Vooraf
Bij elke 1000ste tik op mijn neus op de homepage een wat ander thema dan normaal em dit was de 42000ste tik.
Ik heb altijd interesse gehad in de vogeltrek. In mijn voorbije jaren als natuurkundedocent mocht ik er altijd graag over vertellen en bovendien, je kunt er in de bovenbouw Atheneum aan rekenen.
Zo is er een of ander pleviertje uit Groenland dat in de herfst – flap, flap, flap – naar acht kilometer hoogte stijgt en daar met de straalstroom mee met een noodvaart naar het Oosten vliegt en in die straalstroom – twiet, twiet, twiet – even met zijn vleugel naar de passerende piloten zwaait (dit op veilige afstand). Ter hoogte van Schotland daalt het beestje, gaat bijtanken in de Waddenzee, en vliegt dan langs gebruikelijke routes naar Afrika.
In het voorjaar vliegt hij weer terug naar de Waddenzee. Daar wacht het beest tot er een geschikt hogedrukgebied langs komt en dan vliegt hij – flap, flap, flap – vlak over de zee, met de wind weer in de rug, terug naar huis.
Toegegeven, het verhaal is enigszins antropomorf gemaakt, maar af en toe moet het een beetje sappig zijn voor de klas.
En, het zij toch maar even gezegd: vliegen is interessant, maar niet met honderdduizenden herrieschoppers en lucht- en klimaataantasters tegelijk.


Rosse grutto B6 vliegt een wereldrecord non stop-vliegen
Ik kreeg inspiratie voor dit artikel toen ik onlangs vernam dat Rosse Grutto B6 een nieuw wereldrecord non stop-vliegen gevestigd had. Bij nader onderzoek bleek dat het wereldrecord er al een tijdje stond, namelijk vanaf okt 2022. Maakt niet uit.
Hierboven hoe een rosse grutto er in het algemeen uit ziet, en hoe rosse grutto B6 er specifiek uitziet toen hij op 15 juli 2022 bij Nome in Alaska geringd werd en van een piepklein zendertje (5 gram, inclusief klein zonnepaneel) voorzien. Daardoor was hij (of zij, dat vermeldt het verhaal niet) met een satelliet te volgen.
Voor meer informatie over de rosse grutto zie https://nl.wikipedia.org/wiki/Rosse_grutto
Vogels vliegen op vet, want dat is de meest energierijke natuurlijke brandstof. Om zover mogelijk te komen laden ze zich zo vol mogelijk, zodanig dat ze soms nauwelijks nog van de grond komen. Het volgewicht van een rosse grutto is 485 gram en het leeggewicht 215 gram.
De rosse grutto verbouwt zichzelf voor de vlucht zelfs van binnen. Zijn lever, nieren en andere ingewanden worden tijdelijk zeer veel kleiner (die heeft hij per slot van rekening onderweg toch niet nodig) en zijn hart en vliegspieren groter – alles gericht op zoveel mogelijk vet meenemen. Na aankomst alles weer andersom.
Een artikel dat dit uitvoerig beschrijft is https://academic.oup.com/auk/article/139/2/ukab086/6523130 . Daarin wordt al vol ontzag gesproken over de vogelprestaties die de natuurwetenschap tot aanpassingen dwongen – dat was dan nog een half jaar voor B6 tot nog meer ontzag leidde (voor wie het artikel wil lezen: de rosse grutto is de Limosa lapponica baueri ). Het meetprogramma onder dit Academic-artikel liep al een tijdje.
De factor (ongeveer) 2 tussen vol- en leeggewicht is overigens gebruikelijk in alles wat vliegt – zelfs een B747 voldoet er aan.
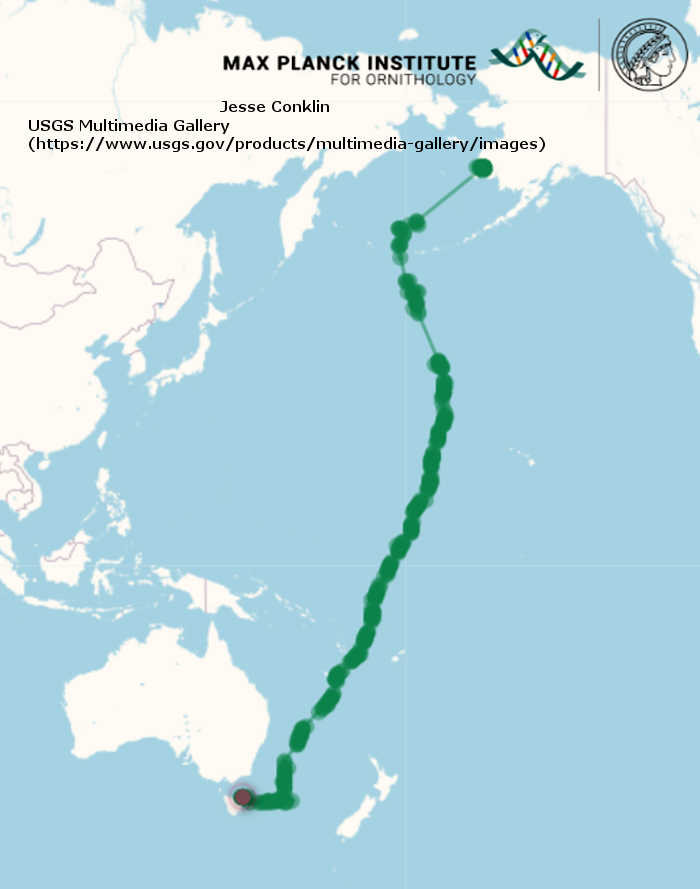
En toen vloog Rosse Grutto B6, net vier maand uit het ei, bovenstaand traject richting Zuid. Het is 13,558 km en dat deed het beest in 11 dagen – non stop vliegend.
Het originele artikel is van de US Geological Survey (USGS), waarvan ook bovenstaande kaart afkomstig is (zie https://www.usgs.gov/centers/alaska-science-center/news/juvenile-bar-tailed-godwit-b6-sets-world-record en vandaar uit https://www.adn.com/alaska-news/wildlife/2022/10/30/a-juvenile-shorebird-tagged-in-alaska-flew-nonstop-for-11-days-and-arrived-in-tasmania/ )
Die elf dagen is het echte schokkende – de afstand hangt er ook van af hoe de wind stond. B6 had hem mogelijk mee, maar dat mag men niet eens geluk noemen want vogels hebben, zoals iemand het in de New York Times het formuleerde, een ‘griezelig vermogen om het weer te voorspellen’ en het zijn uitstekende navigatoren – zodanig dat de oude Polynesische zeevaarders, ook niet mis, vogelgedrag in hun intellectuele pakket hadden als ondersteuning. (Het artikel in de New York Times op The Godwit’s 7,000-Mile Journey: A Migration That Breaks Records – The New York Times .)
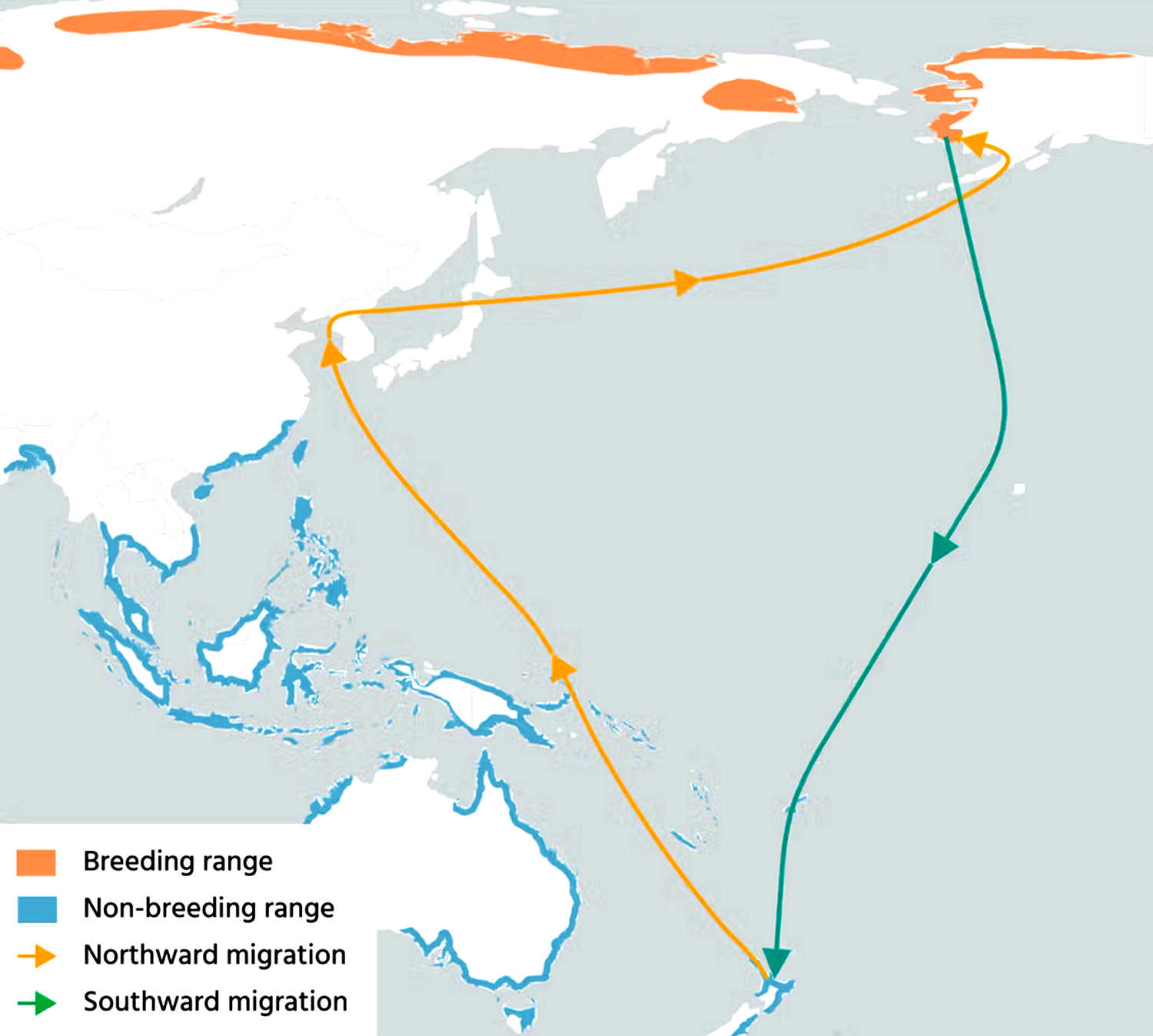
Rosse grutto’s vliegen terug over de Gele Zee (bij China en Korea), waar ze een paar weken bij tanken alvorens weer naar Alaska te gaan ( https://datazone.birdlife.org/articles/the-bar-tailed-godwit-undertakes-one-of-the-avian-worlds-most-extraordinary-migratory-journeys ).
Men schat dat een rosse grutto in zijn leven zowat een half miljoen kilometer vliegt.
De parkiet van Tucker
Hierbij moet eerst het prachtige boek van hoogleraar Henk Tennekes (de meteoroloog) genoemd worden “De wetten van de vliegkunst” (1992), later bewerkt tot “The Simple Science of Flight, Revised and Expanded Edition” ( archive-MITpress ) . Onderstaand verhaal komt via zijn boek.
Professor Vance Tucker had een parkiet getraind om met een zuurstofmaskertje op in een windtunnel te vliegen. De windsnelheid en de hellingshoek kon hij instellen. Men zegt dat het vogeltje wekenlang gewillig meewerkte – hij zal er wel heel goed voor gezorgd hebben. En dat terwijl een parkiet geen goede vlieger is.
Via de zuurstof kon hij, gebruikmakend van wat gangbare extra aannames, het mechanisch vermogen van het vogeltje berekenen bij de ingestelde omstandigheden. Hieronder de geschematiseerde opstelling en daaronder de resultaten. Die zijn voor dit concrete parkeitje, maar met andere getallen gelden ze voor alle vogels (behalve mogelijk kolibries).
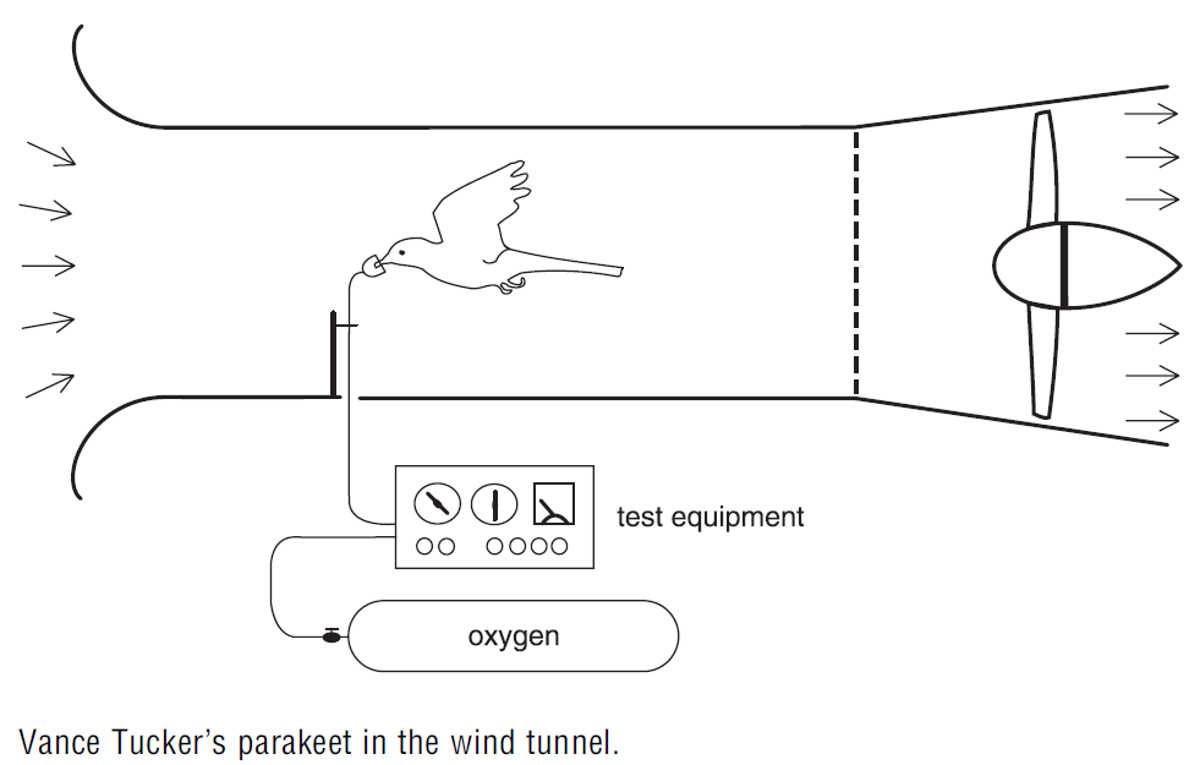
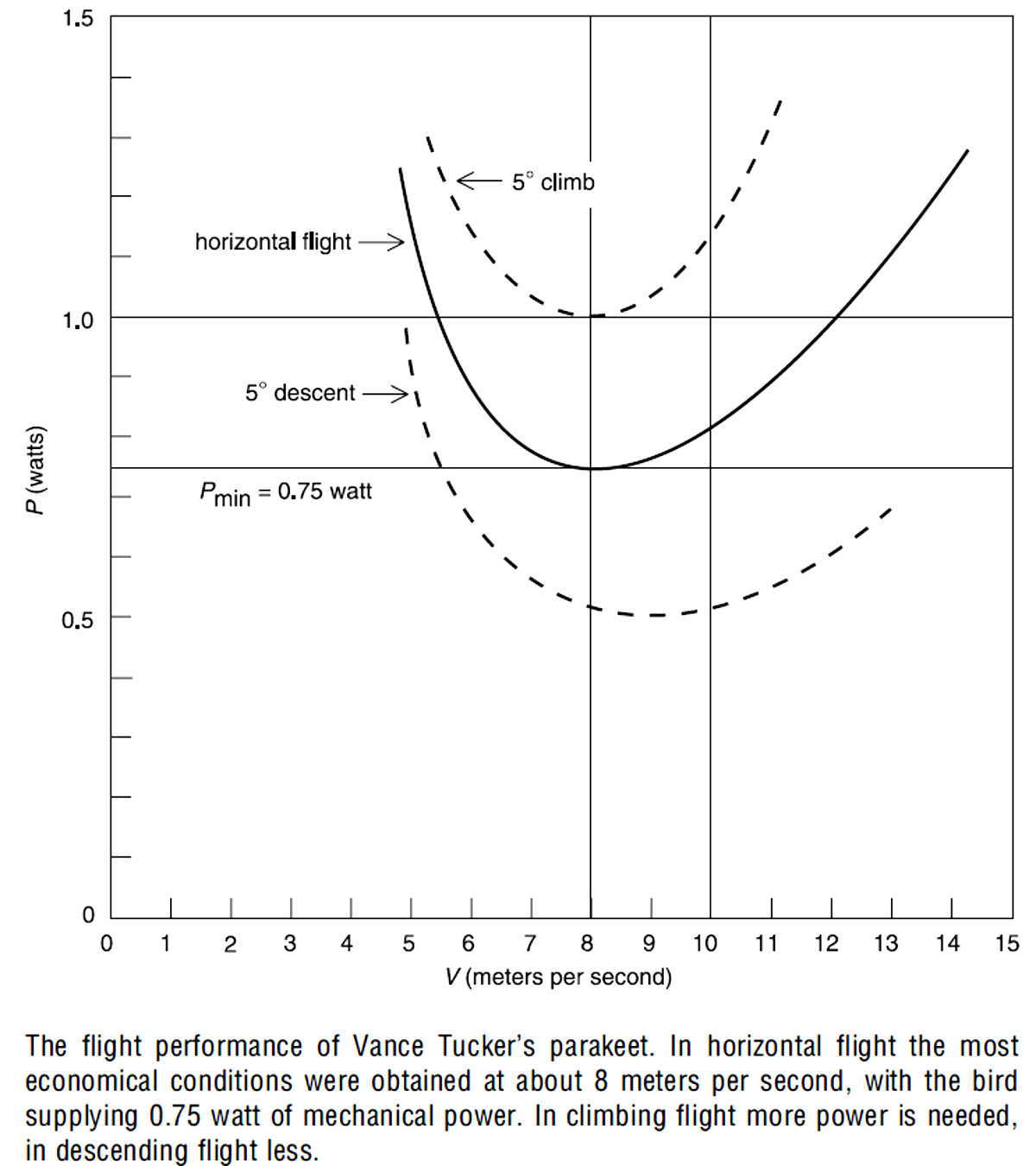
De algemeen geldende conclusie is dat alle vogels bij een bepaalde snelheid het makkelijkste vliegen. Tuckers parkietje heeft in horizontale vlucht het laagste vliegvermogen nodig (nl 0,75W) bij 8,0m/sec. Zowel langzamer als sneller vliegen vraagt meer vermogen, evenals uiteraard schuin omhoog vliegen.
Voor dit optimale punt is een ‘glijgetal’ gedefinieerd. Dat is bij een constante horizontale snelheid een verhoudingsgetal tussen enerzijds de lift = de zwaartekracht en anderzijds de luchtwrijving = de spierkracht. Tevens is dit (vandaar de naam) het aantal horizontale meters dat een vogel in glijvlucht aflegt per één verticale meter.
Veel zangvogels hebben een glijgetal in de buurt van de 4 . Dat betekent zowel dat de spierkracht een kwart van de zwaartekracht is als dat de vogel, als hij zijn vleugels stilhoudt, per meter daling vier meter vooruit komt.
Een parkiet en een fazant hebben een glijgetal van ongeveer 4, een gierzwaluw van ca 10, een albatros van ca 22, een passagiersvlieegtuig heeft een glijgetall van 15 tot 20 (dus als op 10km hoogte alle motoren uitvallen, komt het nog een aardig eind vooruit), een zweefvliegtuig van 20 tot 60.

Veldleeuwerik
Rekenen aan een leeuwerik (en dat correctiemodellen nooit waterdicht zijn)
Ik had in mijn tijd als natuurkundeleraar een som gemaakt hoever een leeuwerik kon vliegen. Een lege (uitgehongerde) leeuwerik is 17 gram, een volgevreten exemplaar 35 gram (dus gemiddeld over de vlucht 26 gram). De aarde trekt eraan met (gemiddeld) 0,26Newton (N) en omdat het glijgetal van een leeuwerik 4 is , moet voor een horizontale vlucht met constante snelheid de voorwaartse kracht een kwart van 0,26N zijn, dus 0,065N .
35 – 17 = 18gram vogelvet bevat een chemische energie van 18*30 = 540kJ (540.000 van de energieeenheid Joule). Bij een spierrendement van 25% wordt van die 540kJ een kwart, dis 135kJ, omgezet in mechanische arbeid en de rest wordt warmte.
Die 135kJ gedeeld door 0,065N is nu de afstand die de leeuwerik kan vliegen. Dat is 2075km.
Daarmee halen ze, bij windstil weer, om en nabij Zuid-Europa, de Balkan of de Noordkust van Afrika en dat schijnt voor de beestjes ver genoeg te zijn.
Dit was dus een opgave die de meeste leerlingen op de bovengeschetste manier konden oplossen. Mooi.
Nu was er een leerling die iets anders bedacht had. Hij liet de leeuwerik (met, voor insiders, 135kJ =mgh) loodrecht opstijgen tot 520km hoogte (ongeveer de hoogte van de Starlink-satellieten van Elon Musk). Van daar af ging het beestje in voorgeschreven glijvlucht (4 op 1) naar beneden en landde keurig op 2075km op de gewenste afstand.
Een goed antwoord op een volstrekt onmogelijke manier, daar voorzag mijn correctiemodel niet in. Uiteindelijk heb ik maar een besluit genomen met een enigszins subjectief karakter en er drie van de vier beschikbare punten voor gegeven,

Gossamer Pinguin

De Zephyr
Alles wat vliegt op één lijn
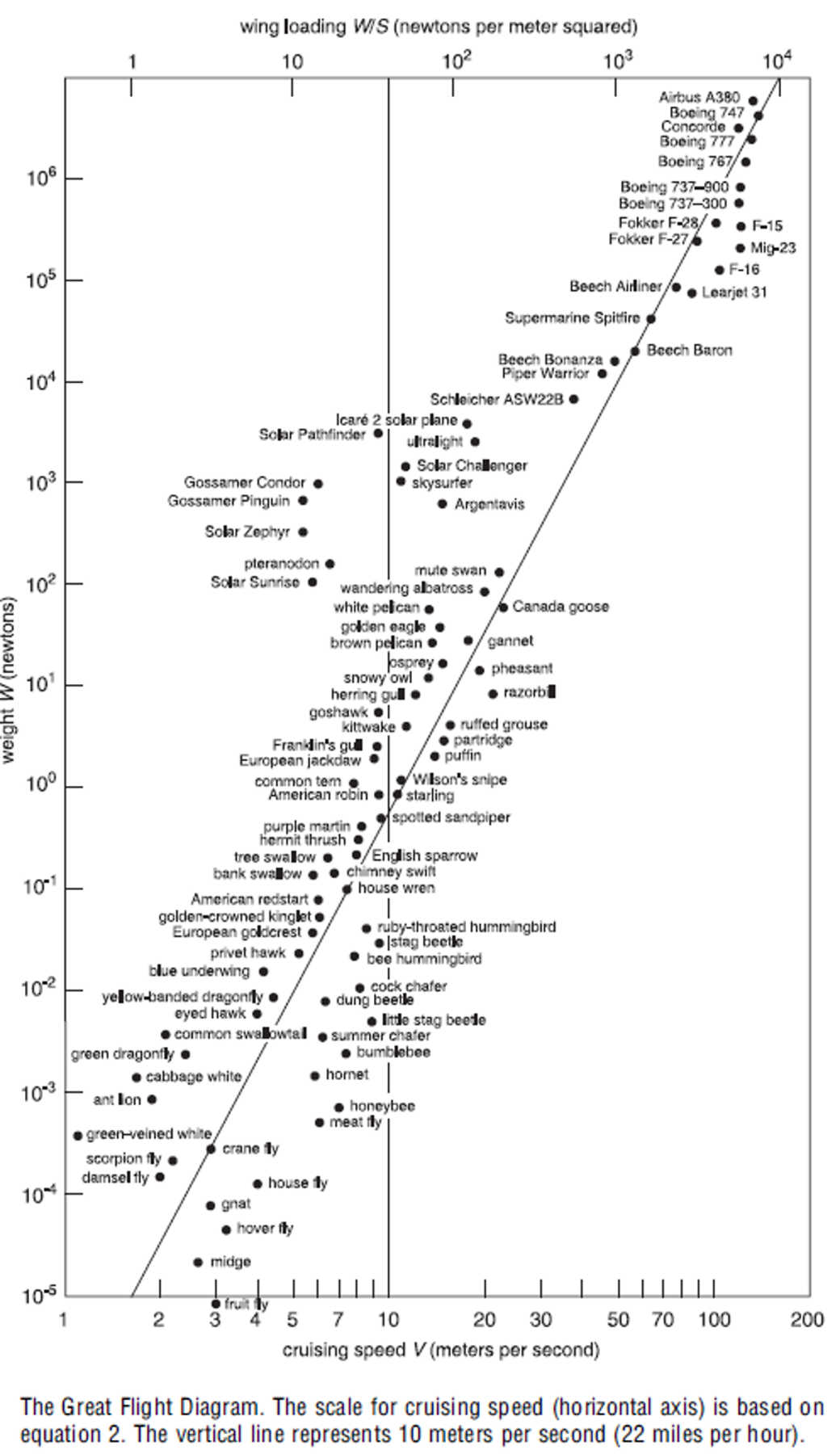
Tot slot een beroemde grafiek uit het boek van Tennekes: van fruitvlieg tot A350 in één (dubbellog) diagram. Zie hieronder.
- Op de horizontale as onder de kruissnelheid in m/sec (bedoeld wordt de meest economische snelheid, zoals boven uitgelegd, op het laagste punt van de U-curves)
- Vertikaal de zwaartekracht op de vogel in Newton (bij de gekozen nauwkeurigheid kun je zeggen dat de aarde aan 1kg trekt met 10N)
- Horizontaal boven de vleugelbelasting (de zwaartekracht op de vleugel (in N) gedeeld door de vleugeloppervlakte (in m2 )
- Alles onder de “mute swan (=knobbelzwaan)” leeft en alles daarboven is dood
- Links van de lijn de typische zwevers, waaronder enkele exotische menselijke constructies (de Gossamer condor is een fietsvliegtuig, zie https://www.wired.com/2010/08/0823gossamer-condor-human-powered-flight/ en de Gossamer Pinguin ook, maar dan met zonnepanelen erop).
De Solar Zephyr is een drone voor militair verkenningsdoeleinden in de stratosfeer, werkend op zonnepanelen ( https://www.aerosociety.com/news/zephyr-down-but-definitely-not-out/ )
Let hier ook op de positie van de Pteranodon (een vliegend reptiel uit het Mesolithicum)
Rechts van de lijn alles wat men snel wil of wat snel moet, zoals de F16 of de, gezien zijn kleine vleugeloppervlak relatief onhandig zware, hommel (bumble bee) of honingbij.